
Question and Answers Forum
Question Number 87488 by jagoll last updated on 04/Apr/20
![sin^4 x + sin^4 (x+(π/4)) = (1/4) x ∈ [ 0,2π ]](Q87488.png)
Commented by john santu last updated on 05/Apr/20
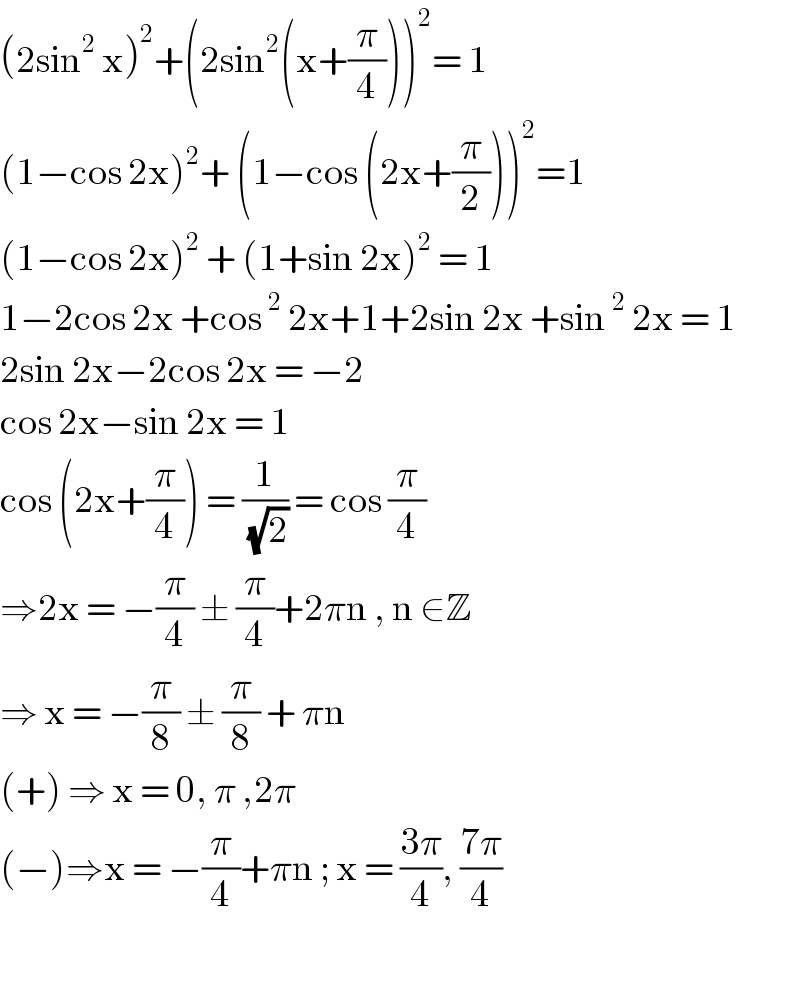
Answered by mind is power last updated on 04/Apr/20
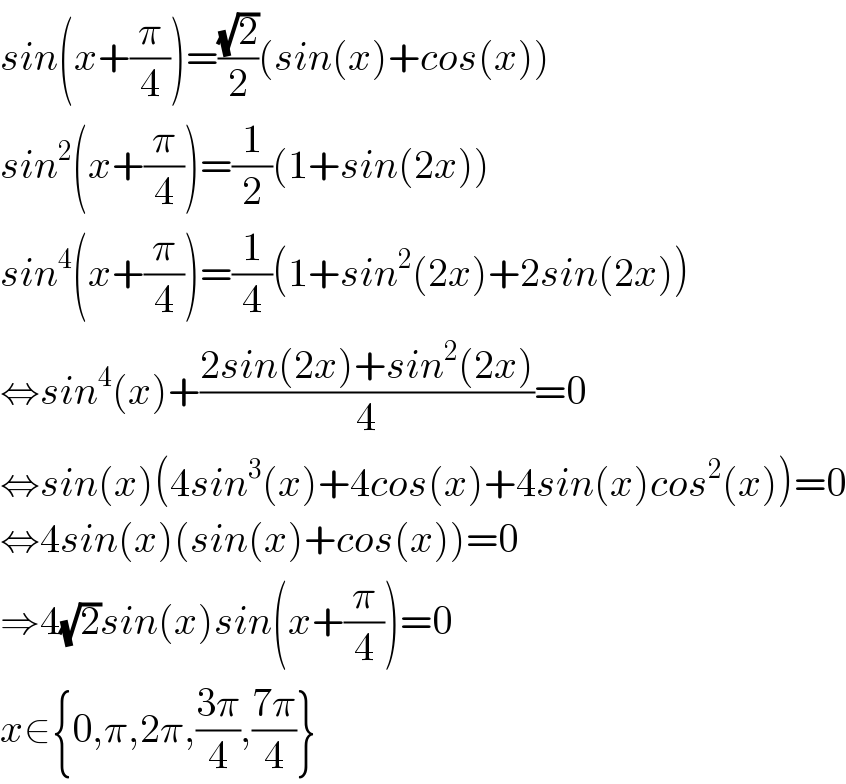
Answered by TANMAY PANACEA. last updated on 04/Apr/20
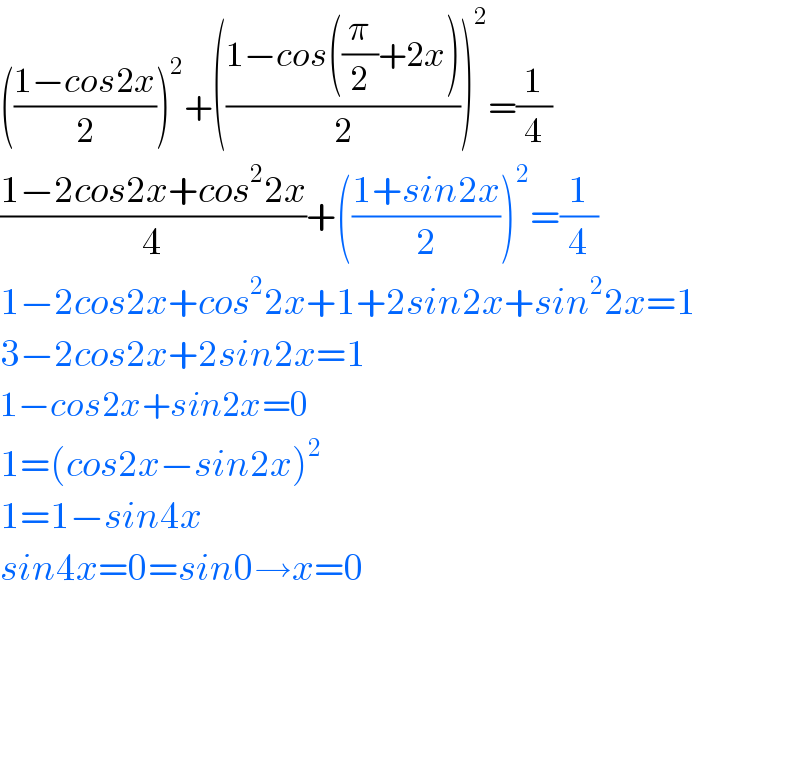
| ||
Question and Answers Forum | ||
Question Number 87488 by jagoll last updated on 04/Apr/20 | ||
![sin^4 x + sin^4 (x+(π/4)) = (1/4) x ∈ [ 0,2π ]](Q87488.png) | ||
Commented by john santu last updated on 05/Apr/20 | ||
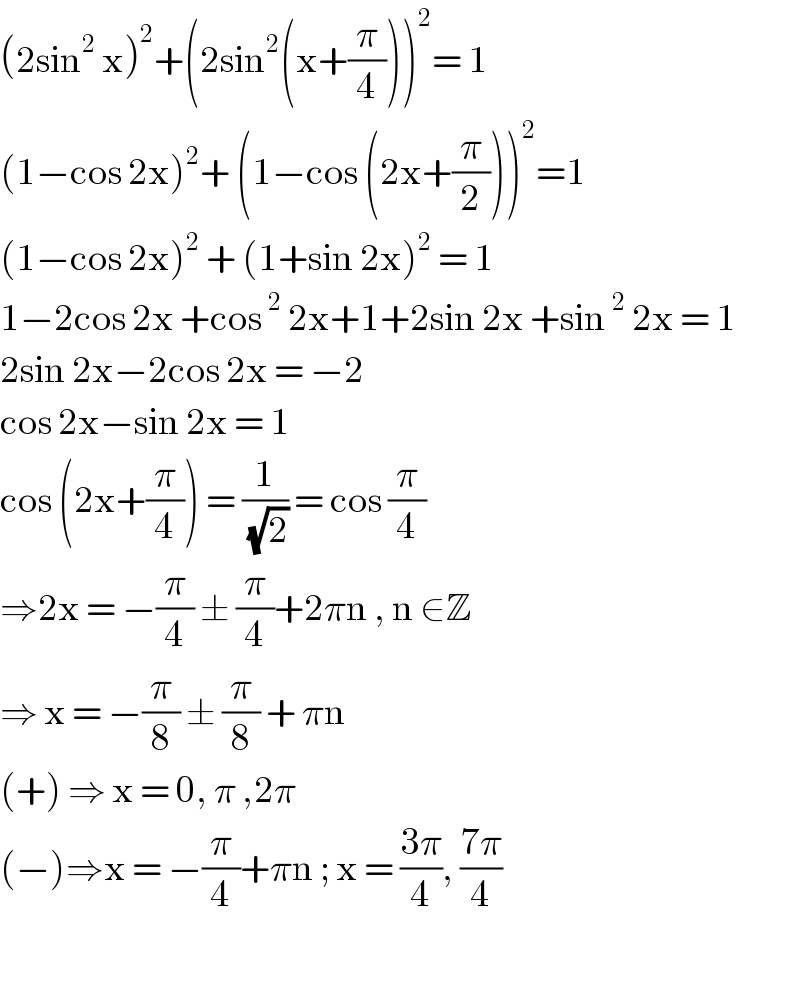 | ||
Answered by mind is power last updated on 04/Apr/20 | ||
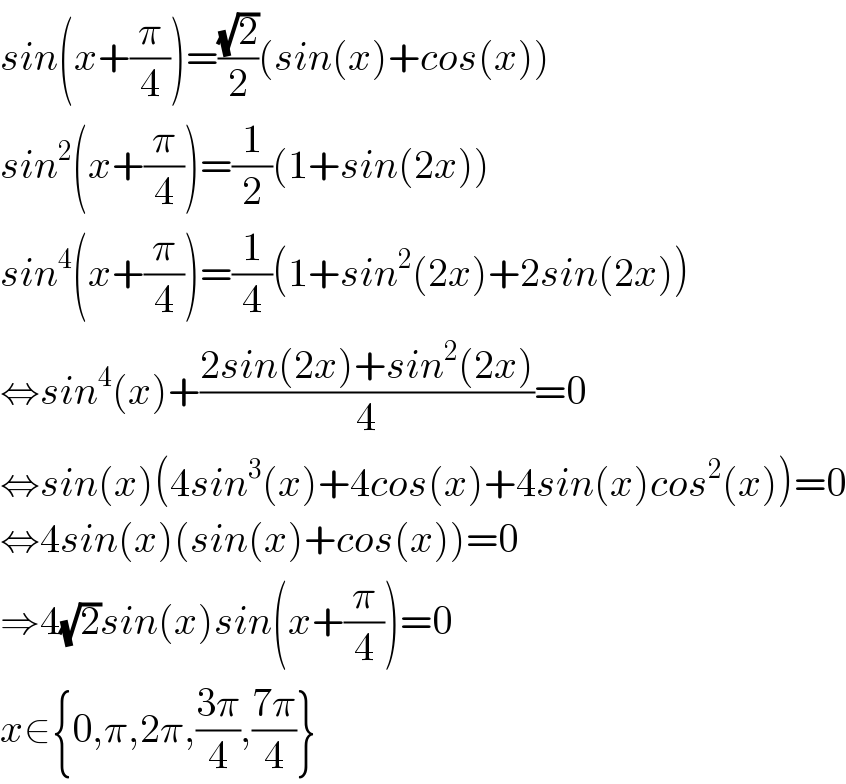 | ||
| ||
Answered by TANMAY PANACEA. last updated on 04/Apr/20 | ||
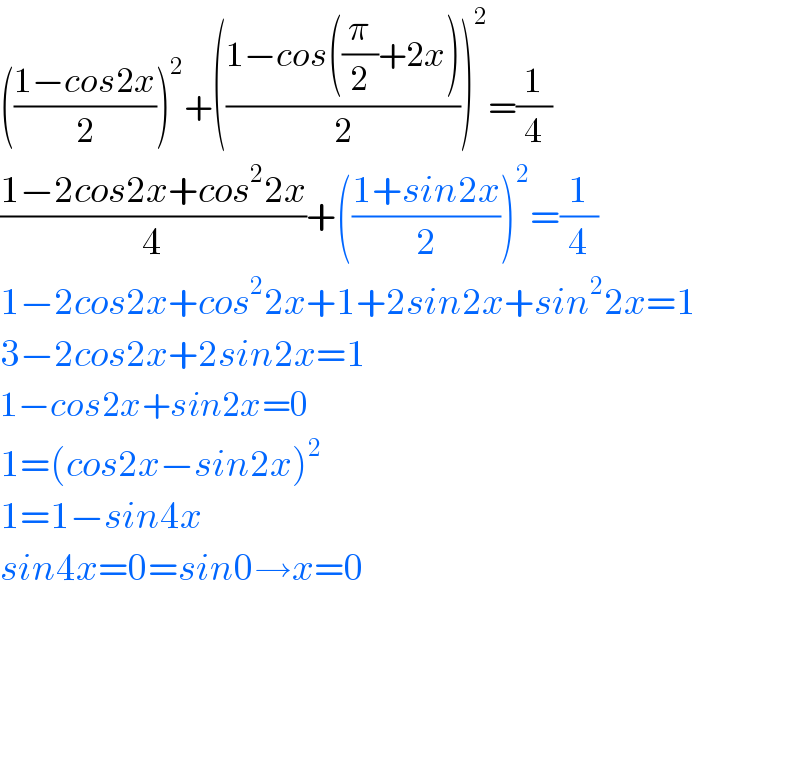 | ||
| ||