
Question and Answers Forum
Question Number 114196 by mathdave last updated on 17/Sep/20
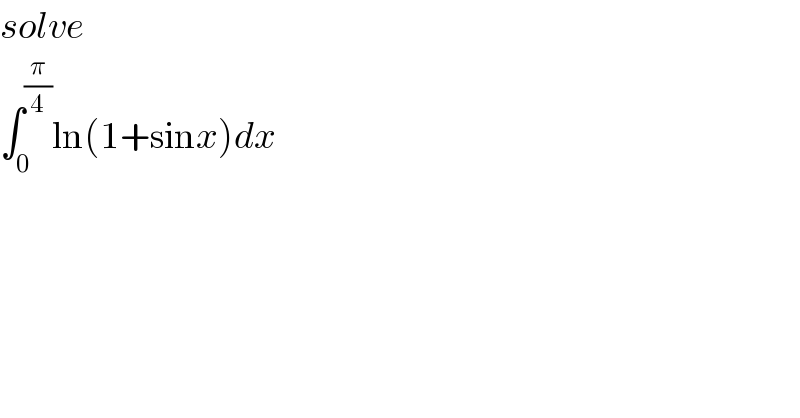
Commented by Dwaipayan Shikari last updated on 20/Sep/20
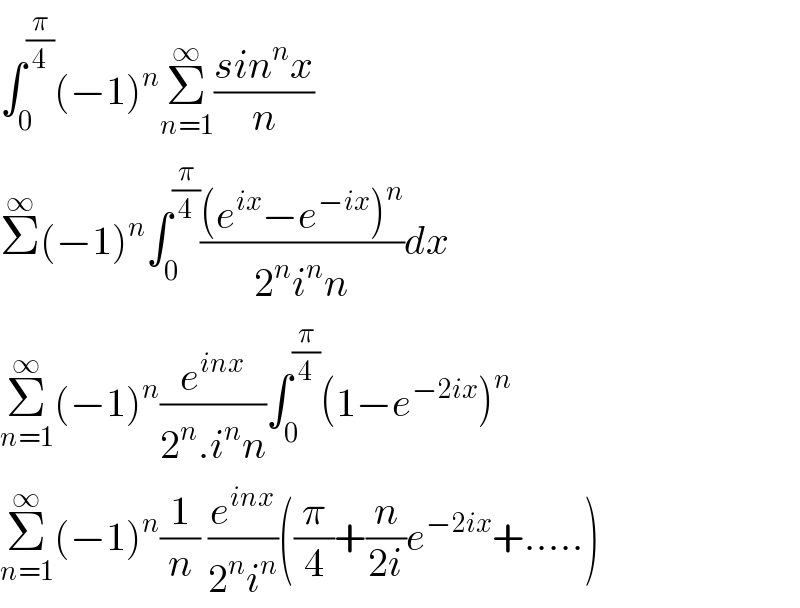
Answered by mathmax by abdo last updated on 19/Sep/20
![let take a try with this integral I =∫_0 ^(π/4) ln(1+cos((π/2)−x))dx =∫_0 ^(π/4) ln(2cos^2 ((π/4)−(x/2)))dx =(π/4)ln(2)+2 ∫_0 ^(π/4) ln(cos((π/4)−(x/2)))dx changement (π/4)−(x/2)=t give ∫_0 ^(π/4) ln(cos((π/4)−(x/2)))dx =∫_(π/4) ^(π/8) ln(cost)(−2dt) =2 ∫_(π/8) ^(π/4) ln(cost)dt =2{ [t ln(cost)]_(π/8) ^(π/4) −∫_(π/8) ^(π/4) t×((−sint)/(cost)) dt} =2{(π/4)ln((1/(√2)))−(π/8)ln(((√(2+(√2)))/2)) } +2 ∫_(π/8) ^(π/4) t tant dt ∫_(π/8) ^(π/4) t tant dt =_(tant =u) ∫_((√2)−1) ^1 ((u arctanu)/(1+u^2 )) du =[(1/2)ln(1+u^2 )arctanu]_((√2)−1) ^1 −∫_((√2)−1) ^1 (1/2)ln(1+u^2 )×(du/(1+u^2 )) =(1/2)ln(2)(π/4)−(1/2)ln(4−2(√2))×(π/8)−(1/2) ∫_((√2)−1) ^1 ((ln(1+u^2 ))/(1+u^2 )) du but ∫_((√2)−1) ^1 ((ln(1+u^2 ))/(1+u^2 ))du =∫_0 ^1 ((ln(1+u^2 ))/(1+u^2 ))du−∫_0 ^((√2)−1) ((ln(1+u^2 ))/(1+u^2 ))du ∫_0 ^1 ((ln(1+u^2 ))/(1+u^2 ))du =_(u=tanθ) ∫_0 ^(π/4) ((ln((1/(cos^2 θ))))/(1+tan^2 θ))(1+tan^2 θ)dθ =−2∫_0 ^(π/4) ln(cosθ)(the value of this integral is known see the platform i dont remember its value) ∫_0 ^((√2)−1) ((ln(1+u^2 ))/(1+u^2 ))du =∫_0 ^((√2)−1) ln(1+u^2 )Σ_(n=0) ^∞ (−1)^n u^(2n) du =Σ_(n=0) ^∞ (−1)^n ∫_0 ^((√2)−1) u^(2n) ln(1+u^2 )du....be continued...](Q114619.png)
| ||
Question and Answers Forum | ||
Question Number 114196 by mathdave last updated on 17/Sep/20 | ||
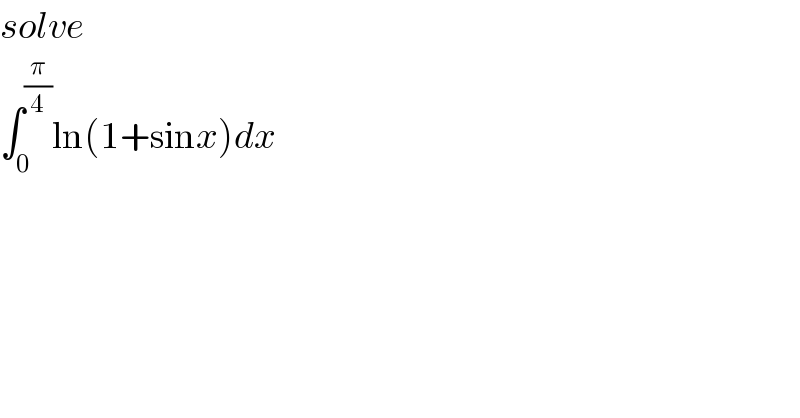 | ||
Commented by Dwaipayan Shikari last updated on 20/Sep/20 | ||
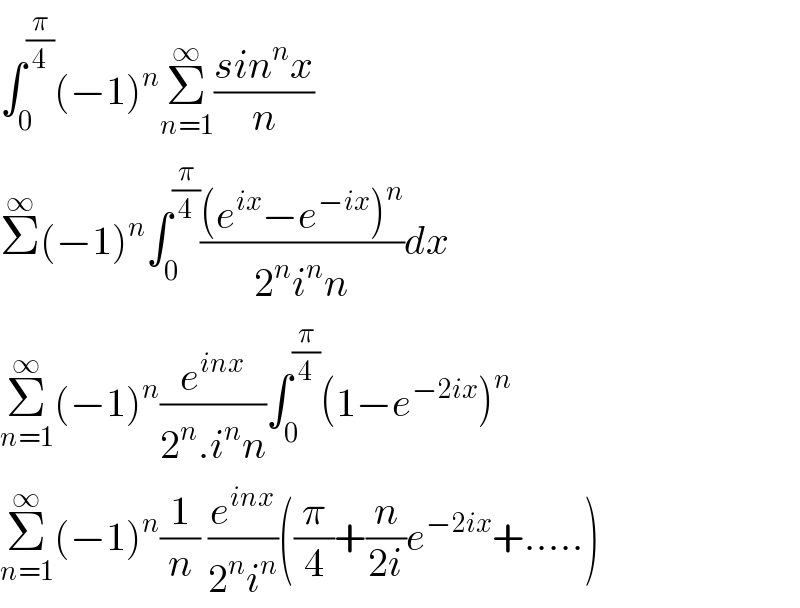 | ||
Answered by mathmax by abdo last updated on 19/Sep/20 | ||
![let take a try with this integral I =∫_0 ^(π/4) ln(1+cos((π/2)−x))dx =∫_0 ^(π/4) ln(2cos^2 ((π/4)−(x/2)))dx =(π/4)ln(2)+2 ∫_0 ^(π/4) ln(cos((π/4)−(x/2)))dx changement (π/4)−(x/2)=t give ∫_0 ^(π/4) ln(cos((π/4)−(x/2)))dx =∫_(π/4) ^(π/8) ln(cost)(−2dt) =2 ∫_(π/8) ^(π/4) ln(cost)dt =2{ [t ln(cost)]_(π/8) ^(π/4) −∫_(π/8) ^(π/4) t×((−sint)/(cost)) dt} =2{(π/4)ln((1/(√2)))−(π/8)ln(((√(2+(√2)))/2)) } +2 ∫_(π/8) ^(π/4) t tant dt ∫_(π/8) ^(π/4) t tant dt =_(tant =u) ∫_((√2)−1) ^1 ((u arctanu)/(1+u^2 )) du =[(1/2)ln(1+u^2 )arctanu]_((√2)−1) ^1 −∫_((√2)−1) ^1 (1/2)ln(1+u^2 )×(du/(1+u^2 )) =(1/2)ln(2)(π/4)−(1/2)ln(4−2(√2))×(π/8)−(1/2) ∫_((√2)−1) ^1 ((ln(1+u^2 ))/(1+u^2 )) du but ∫_((√2)−1) ^1 ((ln(1+u^2 ))/(1+u^2 ))du =∫_0 ^1 ((ln(1+u^2 ))/(1+u^2 ))du−∫_0 ^((√2)−1) ((ln(1+u^2 ))/(1+u^2 ))du ∫_0 ^1 ((ln(1+u^2 ))/(1+u^2 ))du =_(u=tanθ) ∫_0 ^(π/4) ((ln((1/(cos^2 θ))))/(1+tan^2 θ))(1+tan^2 θ)dθ =−2∫_0 ^(π/4) ln(cosθ)(the value of this integral is known see the platform i dont remember its value) ∫_0 ^((√2)−1) ((ln(1+u^2 ))/(1+u^2 ))du =∫_0 ^((√2)−1) ln(1+u^2 )Σ_(n=0) ^∞ (−1)^n u^(2n) du =Σ_(n=0) ^∞ (−1)^n ∫_0 ^((√2)−1) u^(2n) ln(1+u^2 )du....be continued...](Q114619.png) | ||
| ||