
Question and Answers Forum
Question Number 110246 by Her_Majesty last updated on 28/Aug/20
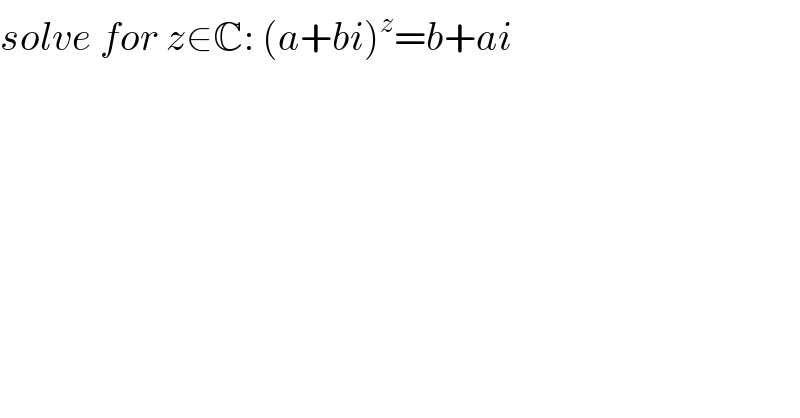
Answered by mr W last updated on 28/Aug/20
![θ=tan^(−1) (b/a) zln (a+bi)=ln (b+ai) z(ln (√(a^2 +b^2 ))+iθ)=ln (√(a^2 +b^2 ))+i((π/2)−θ) z=((ln (√(a^2 +b^2 ))+i((π/2)−θ))/(ln (√(a^2 +b^2 ))+iθ)) z=(([ln (√(a^2 +b^2 ))+i((π/2)−θ)][ln (√(a^2 +b^2 ))+iθ])/(ln^2 (√(a^2 +b^2 ))+θ^2 )) z=((ln^2 (√(a^2 +b^2 ))+((π/2)−θ)θ+(π/2)ln (√(a^2 +b^2 ))i)/(ln^2 (√(a^2 +b^2 ))+θ^2 ))](Q110270.png)
Commented by Her_Majesty last updated on 28/Aug/20

| ||
Question and Answers Forum | ||
Question Number 110246 by Her_Majesty last updated on 28/Aug/20 | ||
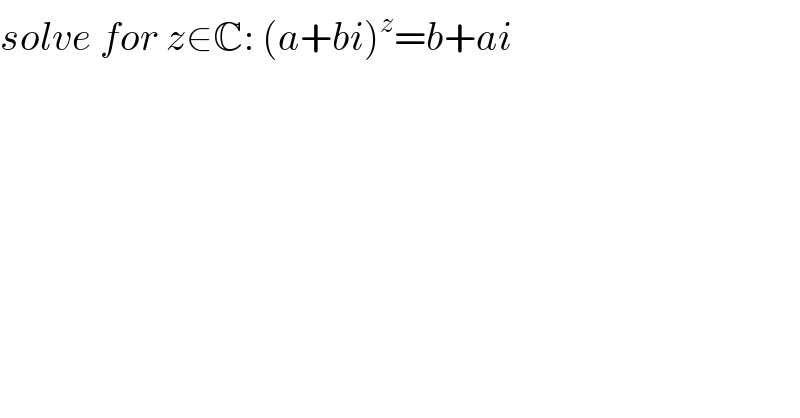 | ||
Answered by mr W last updated on 28/Aug/20 | ||
![θ=tan^(−1) (b/a) zln (a+bi)=ln (b+ai) z(ln (√(a^2 +b^2 ))+iθ)=ln (√(a^2 +b^2 ))+i((π/2)−θ) z=((ln (√(a^2 +b^2 ))+i((π/2)−θ))/(ln (√(a^2 +b^2 ))+iθ)) z=(([ln (√(a^2 +b^2 ))+i((π/2)−θ)][ln (√(a^2 +b^2 ))+iθ])/(ln^2 (√(a^2 +b^2 ))+θ^2 )) z=((ln^2 (√(a^2 +b^2 ))+((π/2)−θ)θ+(π/2)ln (√(a^2 +b^2 ))i)/(ln^2 (√(a^2 +b^2 ))+θ^2 ))](Q110270.png) | ||
| ||
Commented by Her_Majesty last updated on 28/Aug/20 | ||
 | ||