
Question and Answers Forum
Question Number 31972 by abdo imad last updated on 17/Mar/18
![solve inside ]−1,1[ the d.e. (√(1−x^2 )) y^′ +y =e^(−2x) .](Q31972.png)
Commented by math khazana by abdo last updated on 15/Aug/18
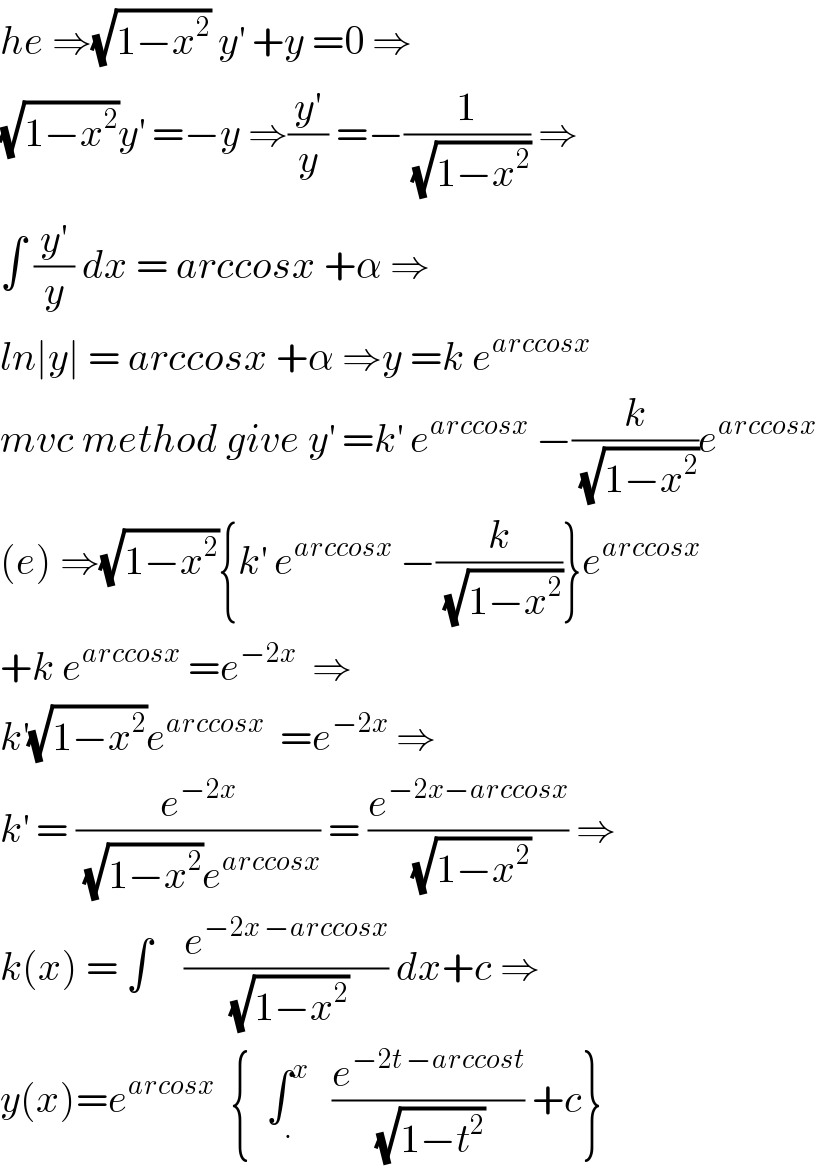
| ||
Question and Answers Forum | ||
Question Number 31972 by abdo imad last updated on 17/Mar/18 | ||
![solve inside ]−1,1[ the d.e. (√(1−x^2 )) y^′ +y =e^(−2x) .](Q31972.png) | ||
Commented by math khazana by abdo last updated on 15/Aug/18 | ||
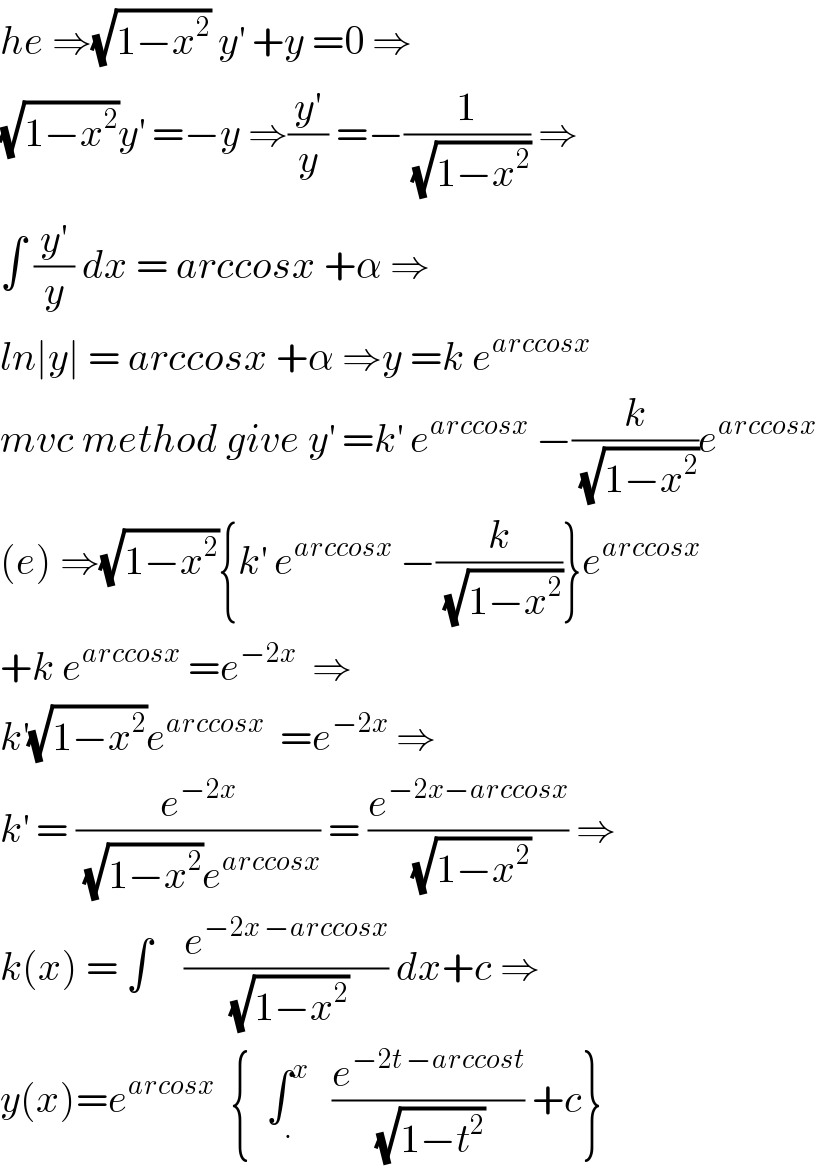 | ||