
Question and Answers Forum
Previous in Relation and Functions Next in Relation and Functions
Question Number 52671 by maxmathsup by imad last updated on 11/Jan/19
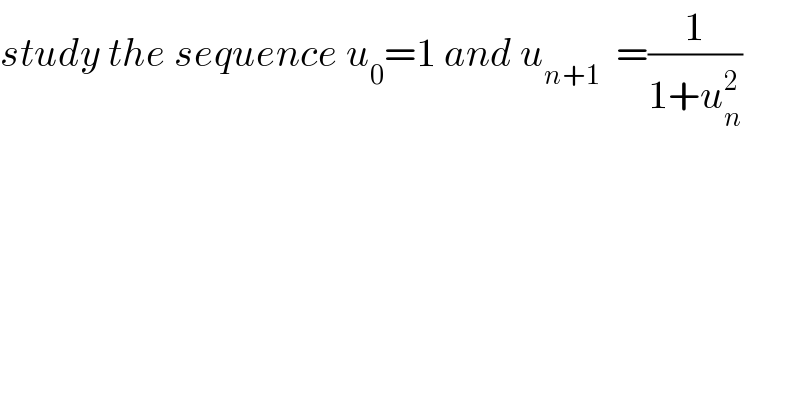
Commented by maxmathsup by imad last updated on 11/Mar/19
![its clear that u_n >0 ∀n let prove that 0<u_n ≤1 n=0 ⇒ 0<u_o ≤1 (true) let suppose 0<u_n ≤1 ⇒ u_(n+1) −1=(1/(1+u_n ^2 )) −1 =−(u_n ^2 /(1+u_n ^2 )) ≤0 ⇒ 0<u_(n+1) ≤1 we have u_(n+1) =f(u_n ) with f(x)=(1/(1+x^2 )) (we can take x>0) ⇒f^′ (x)=−((2x)/(1+x^2 ))<0 ⇒ f is decresing x 0 +∞ f^′ (x) − f(x)1 decre 0 is f have a fixed point f(x)=x ⇒(1/(1+x^2 )) =x ⇒1 =x +x^3 ⇒x^3 +x−1 =0 let p(x) =x^3 +x−1 we have p^′ (x)=3x^2 +1>0 ⇒p is incressing p(0)=−1 <0 and p(1) =1 >0 ⇒∃! α_0 ∈]0,1[ /p(α_0 )=0 and α is the fixed point ⇒ α_0 =lim_(n→+∞) u_n](Q56197.png)
| ||
Question and Answers Forum | ||
Previous in Relation and Functions Next in Relation and Functions | ||
Question Number 52671 by maxmathsup by imad last updated on 11/Jan/19 | ||
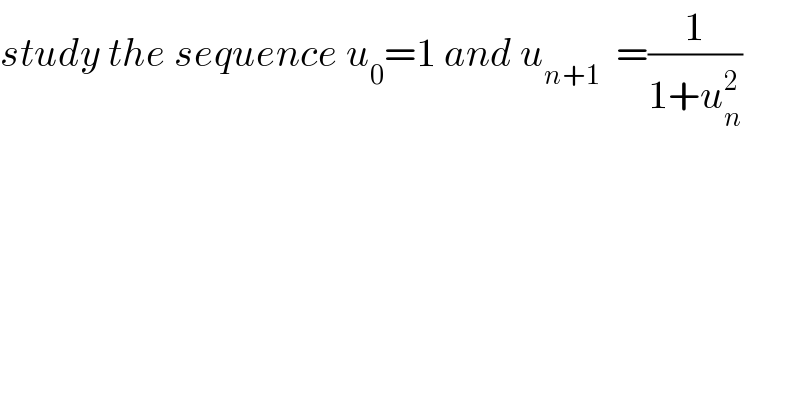 | ||
Commented by maxmathsup by imad last updated on 11/Mar/19 | ||
![its clear that u_n >0 ∀n let prove that 0<u_n ≤1 n=0 ⇒ 0<u_o ≤1 (true) let suppose 0<u_n ≤1 ⇒ u_(n+1) −1=(1/(1+u_n ^2 )) −1 =−(u_n ^2 /(1+u_n ^2 )) ≤0 ⇒ 0<u_(n+1) ≤1 we have u_(n+1) =f(u_n ) with f(x)=(1/(1+x^2 )) (we can take x>0) ⇒f^′ (x)=−((2x)/(1+x^2 ))<0 ⇒ f is decresing x 0 +∞ f^′ (x) − f(x)1 decre 0 is f have a fixed point f(x)=x ⇒(1/(1+x^2 )) =x ⇒1 =x +x^3 ⇒x^3 +x−1 =0 let p(x) =x^3 +x−1 we have p^′ (x)=3x^2 +1>0 ⇒p is incressing p(0)=−1 <0 and p(1) =1 >0 ⇒∃! α_0 ∈]0,1[ /p(α_0 )=0 and α is the fixed point ⇒ α_0 =lim_(n→+∞) u_n](Q56197.png) | ||