
Question and Answers Forum
Question Number 33979 by abdo imad last updated on 28/Apr/18
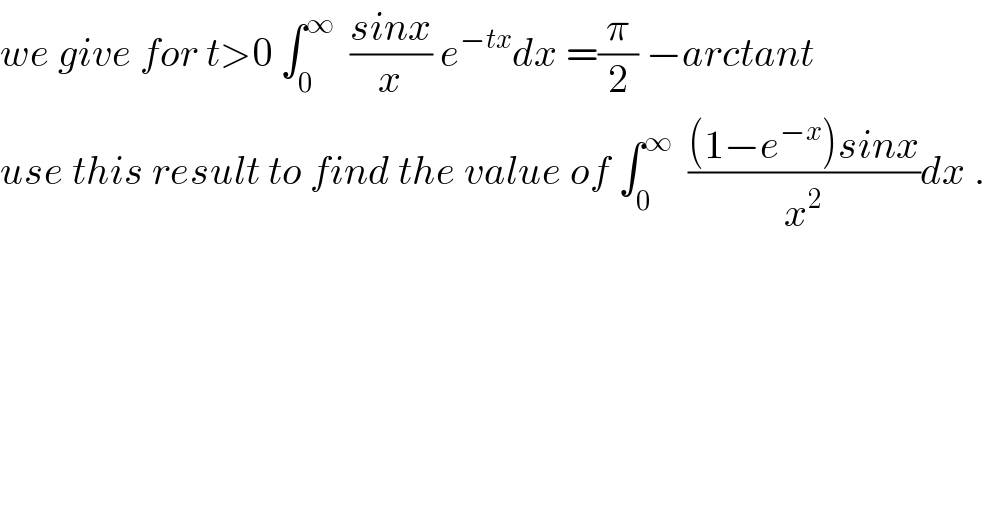
Commented by abdo mathsup 649 cc last updated on 03/May/18
![we know that ∫_0 ^∞ ((sinx)/x) e^(−tx) dx=(π/2) −arctant ⇒ ∫_0 ^1 ((π/2) −arctant)dt = ∫_0 ^1 ( ∫_0 ^∞ ((sinx)/x) e^(−tx) dx) =∫_0 ^∞ (∫_0 ^1 e^(−tx) dt) ((sinx)/x)dx ( by fubini) =∫_0 ^∞ ([−(1/x) e^(−tx) ]_(t=0) ^(t=1) )((sinx)/x)dx =∫_0 ^∞ (1/x^2 )(1−e^(−x) ) sinx dx but ∫_0 ^1 ( (π/2) −arctant)dt =(π/2) −∫_0 ^1 arctan t dt by parts ∫_0 ^1 arctan t dt = [tarctant]_0 ^1 −∫_0 ^1 (t/(1+t^2 ))dt =(π/4) −(1/2)[ln(1+t^2 )]_0 ^1 = (π/4) −(1/2)ln(2) ⇒ ∫_0 ^∞ (((1−e^(−x) )sinx)/x^2 ) dx = (π/4) +(1/2)ln(2) .](Q34235.png)
| ||
Question and Answers Forum | ||
Question Number 33979 by abdo imad last updated on 28/Apr/18 | ||
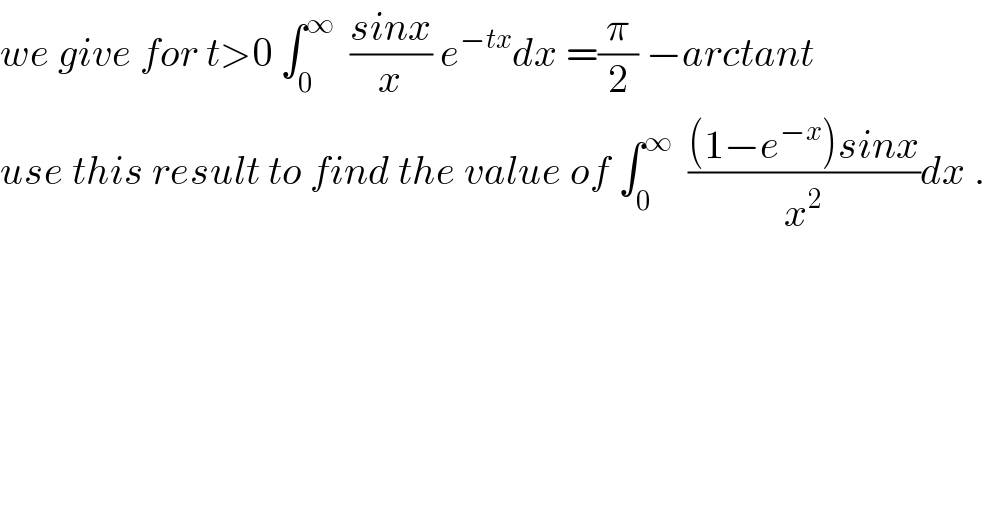 | ||
Commented by abdo mathsup 649 cc last updated on 03/May/18 | ||
![we know that ∫_0 ^∞ ((sinx)/x) e^(−tx) dx=(π/2) −arctant ⇒ ∫_0 ^1 ((π/2) −arctant)dt = ∫_0 ^1 ( ∫_0 ^∞ ((sinx)/x) e^(−tx) dx) =∫_0 ^∞ (∫_0 ^1 e^(−tx) dt) ((sinx)/x)dx ( by fubini) =∫_0 ^∞ ([−(1/x) e^(−tx) ]_(t=0) ^(t=1) )((sinx)/x)dx =∫_0 ^∞ (1/x^2 )(1−e^(−x) ) sinx dx but ∫_0 ^1 ( (π/2) −arctant)dt =(π/2) −∫_0 ^1 arctan t dt by parts ∫_0 ^1 arctan t dt = [tarctant]_0 ^1 −∫_0 ^1 (t/(1+t^2 ))dt =(π/4) −(1/2)[ln(1+t^2 )]_0 ^1 = (π/4) −(1/2)ln(2) ⇒ ∫_0 ^∞ (((1−e^(−x) )sinx)/x^2 ) dx = (π/4) +(1/2)ln(2) .](Q34235.png) | ||