Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 69607 by malwaan last updated on 25/Sep/19

$$\mathit{w}\mathit{i}\mathit{t}\mathit{h}\mathit{o}\mathit{u}\mathit{t}\mathit{u}\mathit{s}\mathit{i}\mathit{n}\mathit{g}\mathit{l}\mathit{h}\mathit{o}\mathit{s}\mathit{p}\mathit{i}\mathit{t}\mathit{a}\mathit{l}\mathit{p}\mathit{l}\mathit{e}\mathit{a}\mathit{s}\mathit{e}$$$$\mathit{p}\mathit{r}\mathit{o}\mathit{v}\mathit{e}\mathit{t}\mathit{h}\mathit{a}\mathit{t}$$$$\underset{\mathit{x}\to 0}{\mathit{l}\mathit{i}\mathit{m}}\frac{\mathit{x}-\mathit{s}\mathit{i}\mathit{n}\mathit{x}}{{\mathit{x}}^3}=\frac{1}{6}$$$$\mathit{I}\mathit{w}\mathit{a}\mathit{n}\mathit{t}\mathit{e}\mathit{v}\mathit{e}\mathit{r}\mathit{y}\mathit{m}\mathit{e}\mathit{t}\mathit{h}\mathit{o}\mathit{d}$$$$\mathit{p}\mathit{o}\mathit{s}\mathit{s}\mathit{i}\mathit{b}\mathit{l}\mathit{e}\mathit{b}\mathit{e}\mathit{c}\mathit{a}\mathit{u}\mathit{s}\mathit{e}\mathit{s}\mathit{o}\mathit{m}\mathit{e}\mathit{o}\mathit{n}\mathit{e}$$$$\mathit{c}\mathit{h}\mathit{a}\mathit{l}\mathit{l}\mathit{e}\mathit{n}\mathit{g}\mathit{e}\mathit{m}\mathit{e}$$

Commented by mathmax by abdo last updated on 26/Sep/19

$$wehavesinx=\sum _{n=0}^{\mathrm{\infty }}\frac{{(-1)}^n{x}^{2n+1}}{(2n+1)!}=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+...\Rightarrow$$$$-sinx=-x+\frac{x^3}{3!}-\frac{x^5}{5!}+\frac{x^7}{7!}+o\left(x^7\right)\Rightarrow x-sinx=$$$$\frac{x^3}{3!}-\frac{x^5}{5!}+\frac{x^7}{7!}+o\left(x^7\right)\Rightarrow \frac{x-sinx}{x^3}=\frac{1}{3!}-\frac{x^2}{5!}+\frac{x^4}{7!}+o\left(x^4\right)\Rightarrow$$$${lim}_{x\to 0}\frac{x-sinx}{x^3}=\frac{1}{3!}=\frac{1}{6}$$

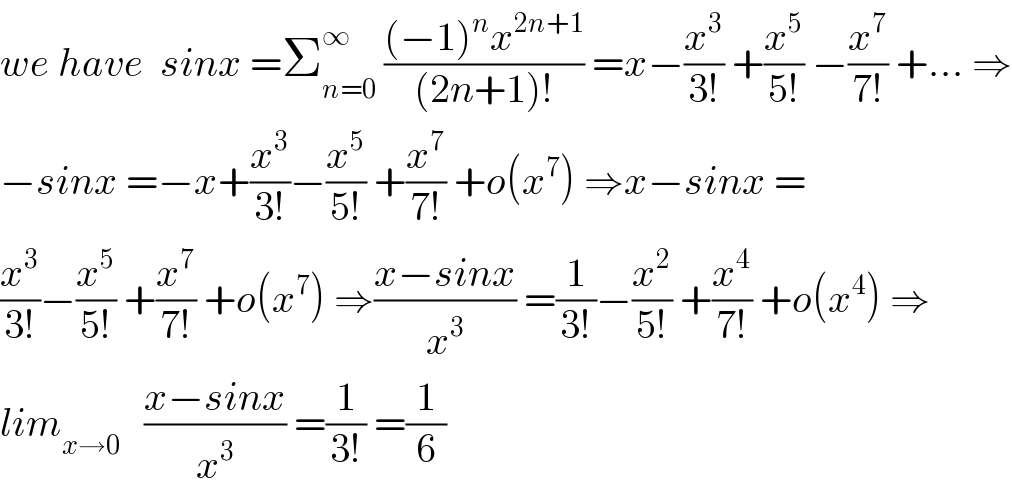
Commented by Prithwish sen last updated on 25/Sep/19

$$\mathrm{li}\underset{\mathrm{x}\to 0}{\mathrm{m}}\frac{\mathrm{x}-(\mathrm{x}-\frac{{\mathrm{x}}^3}{3!}+\frac{{\mathrm{x}}^5}{5!}-....)}{{\mathrm{x}}^3}=\mathrm{li}\underset{\mathrm{x}\to 0}{\mathrm{m}}\frac{1}{3!}-\frac{{\mathrm{x}}^2}{5!}+\mathrm{the}\mathrm{higher}\mathrm{power}\mathrm{of}\mathrm{x}$$$$=\frac{1}{3!}=\frac{1}{6}\mathbf{proved}$$

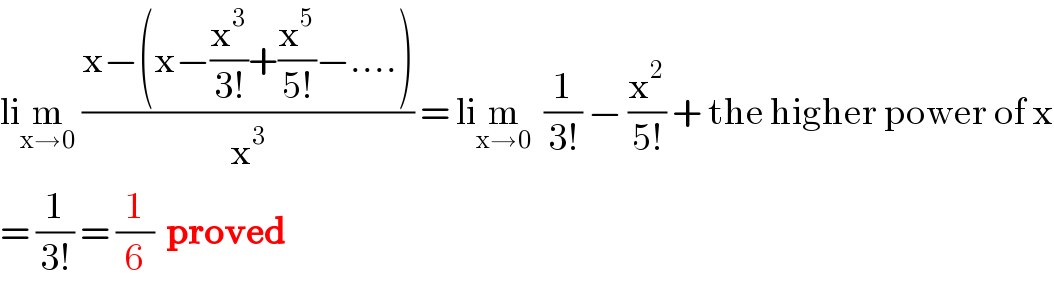
Commented by malwaan last updated on 26/Sep/19

$$thankyousir$$

Commented by malwaan last updated on 27/Sep/19

$$thankyousomuch$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com